Logistic Regression

Lecture 18

Dr. Elijah Meyer

Duke University
STA 199 - Summer 2023

2023-10-31

Happy Halloween

Super Scary

Checklist

– Clone ae-17

– HW-5 due tonight

– Check Slack for formatting tips

– Schedule Change: Project Draft pushed back to Nov 15th

Feedback for draft will be in Issues tab on GitHub

Must respond to / close Issues specific to your selected data set

Looking Forward

Logistic Regression (Today)

Statistical Inference

– Hypothesis Testing

– Confidence Intervals

Statistical Inference: Hypothesis Testing

Your research question can evolve in 199 a bit as we expand our statistical tool-kit:

– Testing if their are meaningful differences between population parameters (i.e., means or proportions)

Example: Penguins

Before, we have modeled the relationship between body mass and island. What if, instead, we wanted to test to see if there is a difference in mean body mass between Penguins on the Dream and Torgersen island?

\(H_o: \mu_{dream} =* \mu_{tor}\)

\(H_a: \mu_{dream} \neq \mu_{tor}\)

Note: You can do something similar with proportions if your response variable is categorical

Statistical Inference: Confidence Intervals

Suppose now instead of testing for a difference, I wanted to estimate what that difference actually is? We can make confidence intervals to estimate a range of plausible values for what \(\mu_{dream} - \mu_{tor}\) actually is.

Note: You can do something similar with proportions if your response variable is categorical

Tool-Kit

Model Data

– Look at relationships; predictions; estimate probabilities (today)

– Hypothesis Testing

– Confidence Intervals

Warm Up

– What is the difference between R-squared and Adjusted R-squared?

— How are each defined?

— When are each appropriate to use?

Warm Up

– How are each defined?

R-squared: The proportion of variability in our response that is explained by our model

Adjusted-R-squared: Measure of overall model fit

Warm Up

— When are each appropriate to use?

R-squared: when the models have the same number of variables

Adjusted-R-squared: when the models have a different number of variables

Goals

– The What, Why, and How of Logistic Regression

– How to fit these types of models in R

– How to calculate probabilities using these models

What is Logistic Regreesion

• Similar to linear regression…. but

• Modeling tool when our response is categorical

Start from the beginning

ae-17

– Motivate why we can not use current techniques to model these types of data

What we will do today

– This type of model is called a generalized linear model

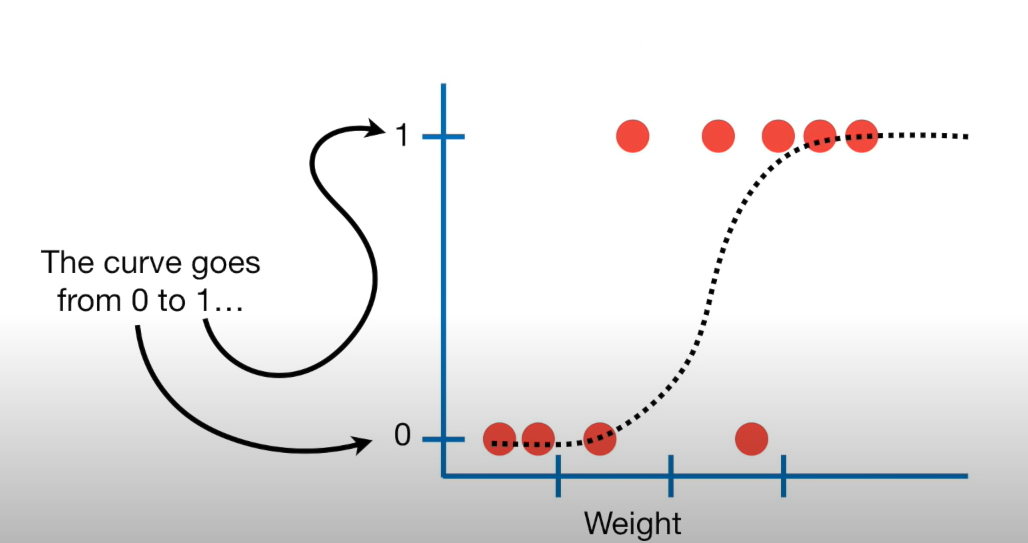
Terms

– Bernoulli Distribution

• 2 outcomes: Success (p) or Failure (1-p)

• \(y_i\) ~ Bern(p)

• What we can do is we can use our explanatory variable(s) to model p

2 Steps

– 1: Define a linear model

– 2: Define a link function

A linear model

\(z_i = \beta_o + \beta_1*X_i + ...\)

Note: We use \(p_i\) for estimated probabilities

We use \(z_i\) as a placeholder for our response variable

• But we can’t stop here… we showed that this doesn’t work…

Next steps

– Preform a transformation to our response variable so it has the appropriate range of values

Generalized linear model

– Next, we need a link function that relates the linear model to the parameter of the outcome distribution i.e. transform the linear model to have an appropriate range

– Or…. takes values between negative and positive infinity and map them to probabilities [0,1]

How we start: Logit Link function

– A logit link function takes values between 0 and 1 and maps it to a value between \(-\infty\) and \(\infty\)

The logit link function is defined as follows:

– Note: log is in reference to natural log

What’s this look like

Takes a [0,1] probability and maps it to log odds (-\(\infty\) to \(\infty\).)

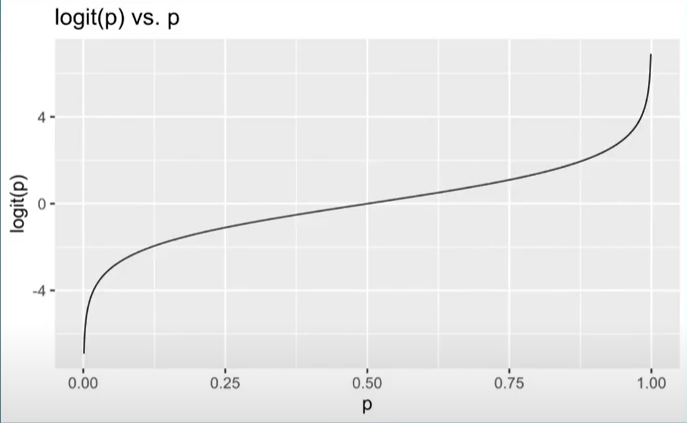
Almost….

This isn’t exactly what we need though…..

Will help us get to our goal

Generalized linear model

– \(logit(p)\) = \(\widehat{\beta_o} +\widehat{\beta}_1X1 + ....\)

– logit(p) is also known as the log-odds

– logit(p) = \(log(\frac{p}{1-p})\)

– \(log(\frac{p}{1-p})\) = \(\widehat{\beta_o} +\widehat{\beta}_1X1 + ....\)

One final fix

– Recall, the goal is to take values between -\(\infty\) and \(\infty\) and map them to probabilities. We need the opposite of the link function… or the inverse

– How do we take the inverse of a natural log?

• Taking the inverse of the logit function will map arbitrary real values back to the range [0, 1]

So

– \(logit(p)\) = \(\widehat{\beta_o} +\widehat{\beta}_1X1 + ....\)

– \[log(\frac{p}{1-p}) = \widehat{\beta_o} +\widehat{\beta}_1X1 + ....\]

– Lets take the inverse of the logit function

– Demo Together

Final Model

\[p = \frac{e^{\widehat{\beta_o} + \widehat{\beta_1}X1 + ...}}{1 + e^{\widehat{\beta_o} + \widehat{\beta_1}X1 + ...}}\]

Example Figure:

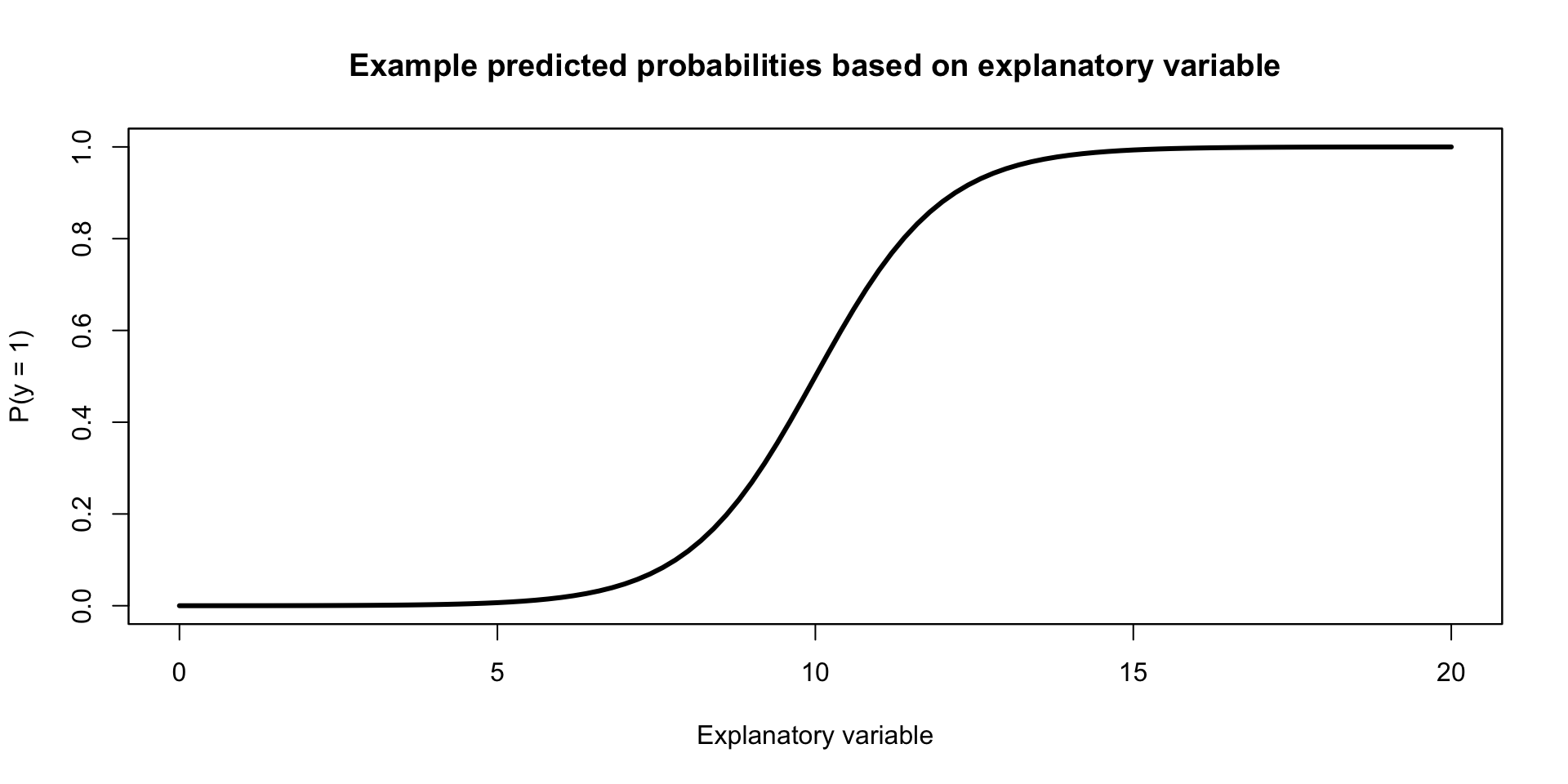
ae-17

Takeaways

– We can not model these data using the tools we currently have

– We can overcome some of the shortcoming of regression by fitting a generalized linear regression model

– We can model binary data using an inverse logit function to model probabilities of success